リッジ回帰
リッジ回帰とは線形回帰の一つで、線形回帰の式に重みの二乗の合計であるL2正則化項を加えたものです。L2正則化項を加えることで、モデルの過学習を抑えることができます。
手法について
リッジ回帰とは、線形化モデルの一種でL2正則化を適用し、罰則をつけながらなるべく多くの変数を用い、多重共線性の影響が少なくなるようパラーメータの推定を行う正則化手法です。
L2正則化とは目的変数に重みの二乗和を加えることで、ほかのデータとは異なる傾向のデータの重みを0に近づけ、モデルを滑らかにします。
そのため回帰係数が大きくなることを防ぎ、過学習を抑えることができます。
手順・式
リッジ回帰では、予測値の誤差の二乗とL2正則化項の合計で予測値が算出されます。
L2正則化項は、ハイパラメータとパラメータ(重み)の二乗和の掛け算で算出されます。L2正則化項では、なるべくパラメータwの絶対値を小さくするような働きをします。ハイパラメータのλはクロスバリデーションもしくは定数の設定により決定します。
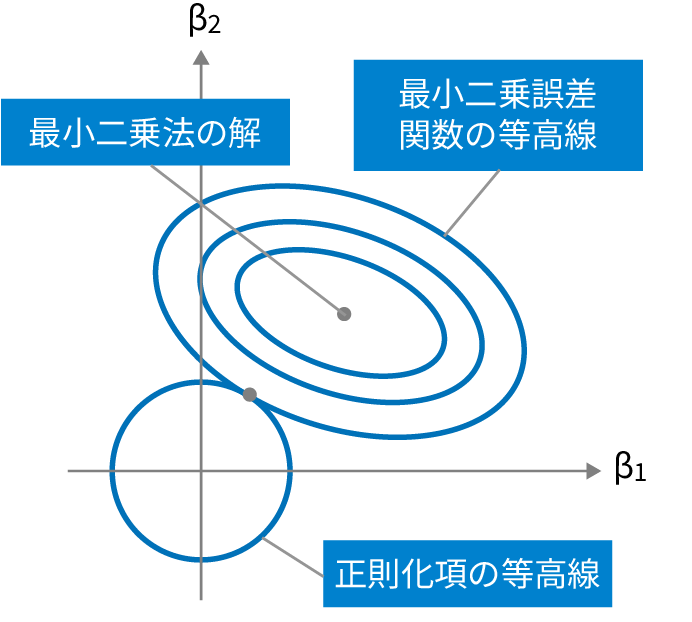
【回帰式】

メリット・デメリット
【メリット】
①過学習を抑えることができる
②多重共線性の問題を解決
正則化することで、多重共線性の問題を解決することができます。
【デメリット】
①モデルが複雑化する可能性がある
正則化で完全に重みが0になるわけではないため、説明変数が非常に多い場合はモデルの解釈が複雑になります。
関連分析技術
ロジスティック回帰 重回帰分析 決定木 ランダムフォレスト XGBoost LightGBM 勾配ブースティング決定木
関連サービス
当社ではこのような機械学習・分析技術を活用した予測モデル、AIモデルの提供を行っています。
・無担保ローン初期審査モデル
・住宅ローン初期審査モデル
・メール配信ターゲット抽出モデル構築
もっと見る
採用情報
機械学習・分析技術で顧客の課題解決に貢献するデータサイエンティストとして働いてみませんか。
ぜひ採用ページもご覧ください。
